| [TOC] | 3.2 Numerical Method Overview | [Prev. Page] | [Next Page] |
The numerical model developed in this thesis uses a method similar in nature to operator-splitting (OS) called integrated operator-splitting (IOS). Integrated operator-splitting was chosen because it allows different reactions to be easily included. This section describes the IOS method used in this model and how it relates to standard OS.
Standard operator-splitting divides equation (3.1) into two parts.
| (3.2) | |
| (3.3) |
The method integrates these equations separately and then recombines them to form equation (3.4) below:
| (3.4) |
Where: D C = change in control volume concentration over a timestep Cf = concentration at end of timestep Co = concentration at beginning of timestep D CA&D = change in concentration due to advection and dispersion D CR = change in concentration due to reactions
Operator-splitting solves the non-reactive solute transport term (D CA&D) first. The result is an intermediate solution (C*) that includes only the effects of advection and dispersion over the time interval D t. It then uses this intermediate solution as the initial concentration to solve the reaction term (D CR) for the concentration at the end of the timestep. Figure 3.2.1 graphically illustrates this process.
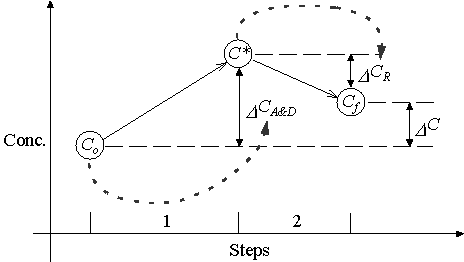
Figure 3.2.1 Standard Operator-Splitting Procedure
The dashed arrows in Figure 3.2.1 illustrate dependencies. In OS D CA&D is a function of the initial concentration, Co. The reaction term, D CR, is a function of the intermediate solution, C*.
Other researchers have used methods similar to the Operator-Splitting method. Kinzelbach and Schäfer (1991) modified the standard OS method to partially re-couple equations (3.2) and (3.3). The value of D CR enters into the solution of the D CA&D term as an added sink/source term in equation (3.2). In turn, D CA&D enters into the solution of D CR as an extra constant sink/source reaction in equation (3.3). Figure 3.2.2 illustrates the dependencies associated with this method of solution.
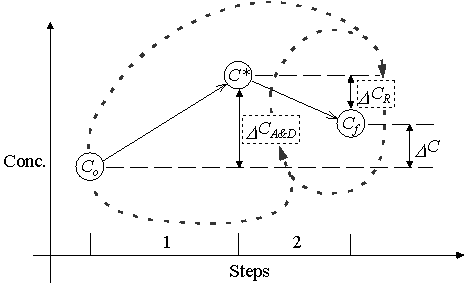
Figure 3.2.2 Operator-Splitting Procedure modified by Kinzelbach
and Schäfer.
Kinzelbach and Schäfer iterate steps 1 and 2 until the final concentration, Cf, converges.
Integrated Operator-Splitting borrows from each of these ideas. The difference between this method and the others is that IOS only re-couples equation (3.3). (See Figure 3.2.3.) The calculation of D CA&D is independent of kinetic reactions. However, D CA&D still enters into the calculation of D CR. In addition, this method makes a distinction between kinetic and equilibrium reactions. D CR is split into two components, kinetic reactions (D CK) and equilibrium reactions (D CE). Also, the model simulates simultaneous movement and reaction of multiple species. Equation (3.5) rewrites equation (3.4) in a form used by IOS.
| (3.5) |
Where: D C = change array of concentration values over a time interval Cf = array of concentration values at end of timestep Co = array of concentration values at beginning of timestep D CA&D = change in concentration array due to solute flux or advection-dispersion D CK = change in array due to kinetic reactions D CE = change in array due to equilibrium reactions
Vector notation is appropriate due to the simulation of multiple species. These species react with each other via kinetic or equilibrium equations. It would be inappropriate to write a separate version of equation (3.5) for each solute since these solutes can be interdependent.
Similar to Kinzelbach and Schäfer’s method, IOS uses an iterative procedure to calculate the concentration at the end of a timestep. Table 3.2.1 and Figure 3.2.3 present this iterative procedure.
Table 3.2.1 IOS Order of Calculation
| Step | Compute | Equation | Comment |
|---|---|---|---|
| 1 | D CA&D | (3.7) | This is computed first, it is only a function of initial concentration and length of time period. Its value will not change between iterations. |
| 2 | Cf | Cf = Co + D CA&D | Compute a trial final concentration, it is needed for the calculation of kinetic reactions. |
| 3 | D CK | (3.9) | Compute the change in concentration due to kinetic reactions, which is a function of initial and final concentrations, and the length of time period. |
| 4 | D CE | (3.10) | Compute the change in concentration due to equilibrium conditions, which is a function of initial concentrations and change in concentration due to flux and kinetic reaction. |
| 5 | D C | (3.5) | Compute the trial change in concentration at the node |
| 6 | Cf | Cf = Co + D C | Compute new trial final concentration. If the change in Cf from the last iteration is not sufficiently small, go back to step 3 and continue iteration. |
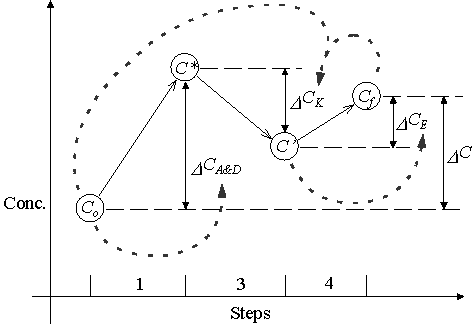
Figure 3.2.2 Integrated Operator-Splitting Procedure
The solution to each term on the right hand side of equation (3.5) uses a different set of underlying assumptions and methods of solution. The change in concentration due to advection and dispersion (D CA&D) is a function of the length of the time step and the concentration at the beginning of the timestep. The model uses a finite difference method corrected for numerical dispersion developed by Poulsen (1994) to solve this term. The solution to the D CA&D term requires the calculation of fluid velocities. The model estimates these velocities using a finite difference technique described later in this section. The change in concentration due to kinetic reactions (D CK) is a function of the time interval length and the concentration at both the beginning and end of the time interval. The linear integrated method described below is used to calculate this term. The change in concentration due to equilibrium reactions is solely a function of the initial concentrations and changes in concentration due to kinetic and flux components (C’).
The following sections describe how the IOS method calculates the components of equation (3.5). The first section describes how the aquifer is discretized. The following section discusses how the model estimates groundwater velocities. A discussion of how the model calculates advective and dispersive fluxes follows in the next section. The subsequent section presents the Linear Integrated method and how it works. Equilibrium calculations appear in the following section. The final section discusses stability criteria. For additional information on the IOS method, see Appendix B.
| [Home] | [Table of Contents] | [Prev. Page] | [Next Page] |
| A Two Dimensional Numerical Model for Simulating the
Movement and Biodegradation of Contaminants in a Saturated Aquifer © Copyright 1996, Jason E. Fabritz. All Rights Reserved. |
|||