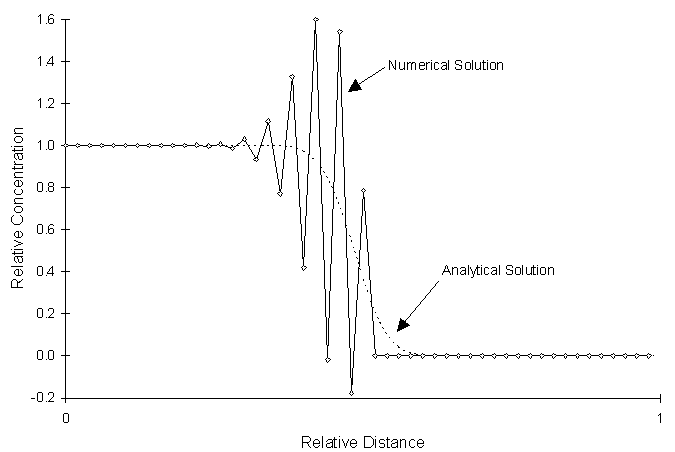
Figure 3.8.1 Unstable Time Oscillations
| [TOC] | 3.8 Oscillations and Stability | [Prev. Page] | [Next Page] |
Like most explicit finite difference schemes, the numerical method outlined above is only conditionally stable (Poulsen, 1994). Under certain conditions, the numerical model is prone to oscillations in space or time. The use of too large of a timestep results in unstable time oscillations. Figure 3.8.1 illustrates time oscillations.

Figure 3.8.1 Unstable Time Oscillations
These oscillations grow larger as the simulation progresses in time, causing the simulation to eventually fail.
Use of too small of a timestep results in stable space oscillations. Unlike time oscillations, space oscillations do not grow as the simulation progresses in time. Figure 3.8.2 illustrates these oscillations.
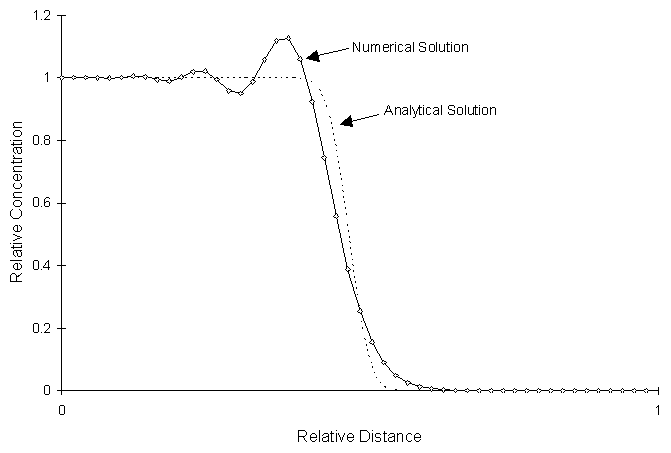
Figure 3.8.2 Stable Space Oscillations
Proper selection of the time step can control both time and space oscillations. This thesis uses the method of Wind and Van Doorne (1975) to determine the maximum allowable timestep to avoid numerical oscillations in time. This method assumes isotropic conditions without sink/source reactions. For space oscillations, this thesis uses a method based on maximum allowable fluxes to determine the minimum allowable timestep. These timestep criteria are a function of advective-dispersive properties; additional adjustment of the timestep may be necessary for the stability of sink/source reactions. Appendix E discusses the details of the timestep calculations.
The maximum and minimum allowable time steps (calculated in Appendix E) to avoid oscillations in a two-dimensional simulation are:
| (3.11) | |
| (3.12) |
Where: A = B = q = darcy velocity (L/T) D t = timestep (T) D x = grid spacing (L) n = material porosity
For the case of a one-dimensional simulation, equations (3.11) and (3.12) simplify to functions of the Courant and Peclet numbers. The criteria in one dimension as a function of Courant and Peclet numbers are:
| (3.13) | |
| (3.14) |
Where: Co = , courant number
Pe = , peclet number
q = darcy velocity (L/T) D t = timestep (T) D x = grid spacing (L) n = material porosity
Figure 3.8.3 illustrates these equations for the one-dimensional case.
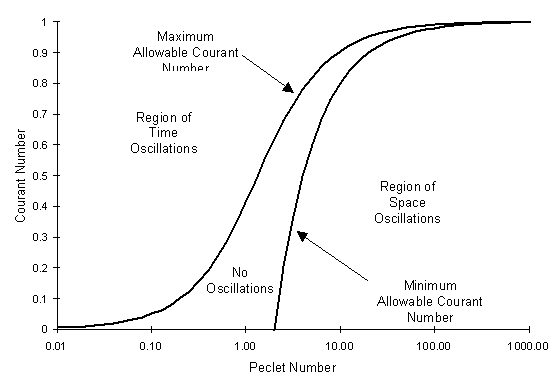
Figure 3.8.3 Maximum and Minimum Courant Number Criteria for one-dimensional
Simulations
Using a time step in the region of no oscillations does not guarantee a perfect solution. There will still be errors associated with the numerical procedure, however they will not be oscillations associated with the time step.
In addition, the timestep criteria was developed under a unique set of assumptions. The timestep criteria assumes uniform aquifer properties; it may not apply to heterogeneous systems. In addition, it does not take sink/source reactions into account. In some cases, it may be necessary to use trial and error to find a suitable time step.
| [Home] | [Table of Contents] | [Prev. Page] | [Next Page] |
| A Two Dimensional Numerical Model for Simulating the
Movement and Biodegradation of Contaminants in a Saturated Aquifer © Copyright 1996, Jason E. Fabritz. All Rights Reserved. |
|||