This chapter provides an overview of the common chemical, biochemical, and solute transport processes that can occur in a saturated aquifer. It includes values reported in literature for parameters and kinetic constants of natural, engineered, and modeled systems where applicable.

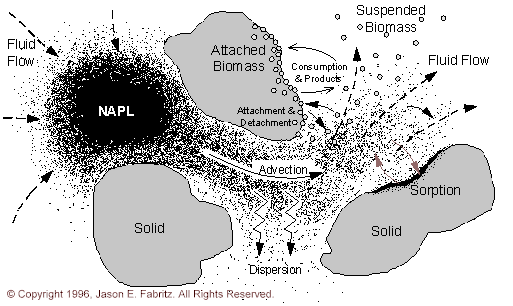
Figure 2.1.1 Iillustrates a conceptual view of the processes occurring in a saturated aquifer.

Figure 2.1.1 Subsurface

A saturated aquifer consists of a porous media, saturating fluid, aqueous and sorbed chemicals and microbes, and sometimes non-aqueous phase liquids (NAPL’s). Pressure gradients (measured as hydraulic head gradients) within the aquifer cause fluid to flow through the porous media. This results in advective transport of aqueous species. Dispersive mixing processes resulting from heterogeneity in the flow field cause solute profiles to "spread" as they move through the aquifer.

Many subsurface processes act as sinks and sources for aqueous species. These processes divide into two major groups: conservative and non-conservative mass transfer processes. Conservative processes transfer mass from one phase to another, conserving total mass. Some examples include the dissolution of NAPL into the aqueous phase and sorption of aqueous species onto immobile porous media. Non-conservative processes transfer mass from one form to another. Some examples are radioactive decay and substrate metabolism by bacteria.

Many recent studies have focused on the role of these non-conservative biological processes in the subsurface. These processes include: substrate consumption, biomass growth, cometabolic transformations, intermediate toxicity, effects on material properties, biomass suspension into the aqueous phase, biomass transport, and biomass movement into the attached phase.

The three major conceptual models explaining the distribution of biomass in the attached phase are Monod, microcolony, and biofilm (Odencrantz, 1992). The Monod model assumes nothing about the distribution of bacteria in the pore space. The bulk concentration of substrates and contaminants drive the biokinetics. The microcolony model assumes microorganisms group themselves in colonies of 10-100 organisms. It assumes that the microcolony sizes are small enough that internal diffusion of substrate to the microorganisms is negligible, making the biokinetics a function of bulk concentration (Odencrantz, 1992). The biofilm model assumes microbes distribute themselves uniformly over the soil particles creating a film. Internal diffusion limits the transport of substrate and contaminants to the microbes in the film.

This thesis uses only Monod type reactions. Monod type reactions are easier to manipulate than the biofilm model and require less input parameters and calibration. Semprini and McCarty (1991, 1993) successfully used Monod kinetics to model in-situ biostimulation and bioremediation at a field site. In addition, Odencrantz (1992) determined that there is little difference in results between the use of Monod and biofilm models for many conditions common to groundwater modeling of natural and engineered systems.

The fundamental equation for advective-dispersive-reactive transport of chemicals and microbes is (Freeze and Cherry, 1979):

(2.1)

Where:	d C/d t = time rate of change in concentration (M/L3·T)
	C = concentration (M/L3)
	D = dispersion coefficient (L2/T)
	V = pore water velocity (L/T)
	R = net rate of reaction (sink/source term) (M/L3·T)

Equation (2.1) consists of two major groups of processes: mass transport and mass transfer. Mass transport includes advective and dispersive transport of aqueous species caused by fluid flow and spatial concentration gradients. Mass transfer includes process such as sorption and biological degradation. The R(C,t) term in Equation (2.1) represents the sum of these transfer processes.