| [TOC] | 2.3 Mass Transfer | [Prev. Page] | [Next Page] |
Mass transfer is the process responsible for the conversion of one component species to another. This process, represented by the R(C,t) term in Equation (2.1), can be the sum of sorption, desorption, decay, abiotic reaction, and metabolism by bacteria. It may also be a function of multiple solutes.
Rate functions typically kinetically limit mass transfer processes. However, in certain circumstances the process proceeds so rapidly relative to the time frame resolution, the process appears to be in equilibrium at all times. These processes are called equilibrium reactions and are mathematically simple compared to their counterparts, kinetic reactions.
Mass transfer processes in a saturated aquifer consist of two major groups: conservative phase transfer processes and non-conservative decay processes. Conservative phase transfer processes are reactions by which mass is transferred from one phase to another. For example, sorption processes move mass between the mobile aqueous phase and the immobile sorbed phase, total mass is always conserved.
The equation representing the rate of transfer between the aqueous phase and sorbed phase is:
| (2.6) |
Where: d Cs/d t = change in sorbed species concentration (M/L3·T) Cs = solute concentration in sorbed phase (M/M) a = rate constant (T-1) Cs* = equilibrium concentration of solute in the solid phase as determined by partitioning equation (M/M)
Two major relationships describe the equilibrium partitioning of aqueous and sorbed species: Freundlich and Langmuir isotherms. Isotherm refers to the relationship holding true at a constant temperature. The Freundlich isotherm is:
| (2.7) |
Where: Cs* = equilibrium solute concentration in the solid phase (M/M) k = partitioning coefficient (L3/M)n n = exponential constant C = concentration of solute in the liquid phase (M/L3)
If n is 1.0, Equation (2.7) reduces to a linear relationship. The partitioning coefficient for the linear case can vary from 0 to 100,000 cm3/g. (See Fry and Istok (1994) for a comprehensive review of linear partitioning coefficients.)
The Langmuir partitioning relationship is:
| (2.8) |
Where: Cs* = equilibrium solute concentration in the solid phase (M/M) Q = partitioning constant (M/M) kL = saturation constant (L3/M) C = concentration of the solute in the liquid phase (M/L3)
Alvarez-Cohen et al. (1993) found that TCE sorption onto a synthetic hydrophobic zeolite in a column study was best represented by the Langmuir relationship where Q = 201 mg/g and kL = 0.521 l/mg.
However, the use of the Langmuir isotherm is not common in most groundwater applications. Many applications involve concentrations at low levels. At these levels, both the Freundlich and Langmuir isotherms approach a linear relationship. In many cases, laboratory data only exists for these low concentrations, resulting in a linear relationship.
Non-conservative decay processes are reactions by which mass is transferred from one type to another. For example, organic substrates are transformed to carbon dioxide. These processes consist of two major sub-groups: abiotic and biological processes. Abiotic processes include chemical reactions not mediated by microbes. For example, radioactive decay is a reaction by which mass changes from one form to another. Total mass of the original species is not conserved. The equation representing the rate of radioactive decay is:
| (2.9) |
Where: d C1/d t = rate of change in decaying species concentration (M/L3·T) d P/d t = rate of change in product concentration (M/L3·T) C1 = concentration of decaying species (M/L3) k = rate constant (T-1) F = Stoichiometric ratio of reactant to product (M/M)
Biologically mediated processes include biomass growth, substrate consumption, products formation, cometabolism, and intermediate toxicity. Since microbes mediate these processes, the mathematical representation is more involved.
Typically two mathematical equations represent a biological process: the rate equation and the stoichiometry equation. The rate equation for a biological process usually yields the rate of primary substrate consumption. The three major rate equations representing primary substrate consumption are single Monod, double Monod, and competitive Monod. (See Appendix A for a discussion of the development of Monod kinetics.)
Single Monod kinetics assume the process is a function of only one limiting substrate. The equation for primary substrate consumption using single Monod kinetics is:
| (2.10) |
Where: k = maximum substrate utilization rate
(M substrate/M cells·T)X = biomass concentration (M/L3) C1 = primary substrate concentration (M/L3) Ks1 = substrate half-saturation constant (M/L3)
There are two special cases that derive from single Monod kinetics: zero order and first order kinetics. Zero-order kinetics assume the limiting substrate in single Monod kinetics is in such excess (C1 >> KS1) that the term drops from the equation. The resulting rate equation is:
| (2.11) |
Where: k = maximum substrate utilization rate (M primary/M cells·T) X = biomass concentration on a pore volume basis (M/L3) C1 = concentration of primary substrate (M/L3)
Zero-order kinetics are infrequently used because most bioremediation applications treat low concentrations of contaminants. A more common simplification of single Monod kinetics is first order kinetics.
First-order kinetics assume the concentration of the limiting substrate in the single Monod relationship is so small compared to the saturation constant (C1 << KS1) that the concentration term in the denominator can be neglected. The resulting rate equation is:
| (2.12) |
Where: k’ = maximum substrate utilization rate (M primary/M cells·T)
(equals k/KS1 of the single Monod Relationship)X = biomass concentration on a pore volume basis (M/L3) C1 = concentration of primary substrate (M/L3)
The use of single Monod or first-order kinetics does not address the situation where two limiting substrates are important (an electron donor and electron acceptor for example). For these cases, double Monod kinetics has been developed.
Double Monod kinetics add an additional limiting substrate to the rate equation. The primary substrate consumption rate is now a function of biomass concentration and two substrates:
| (2.13) |
Where: k = maximum substrate utilization rate
(M primary/M cells·T)X = biomass concentration on a pore volume basis (M/L3) C1 = concentration of the primary substrate (M/L3) C2 = concentration of the secondary substrate (M/L3) KS1 = primary substrate half saturation constant (M/L3) KS2 = secondary substrate half saturation constant (M/L3)
This relationship is generally used when the secondary substrate (C2) is only available at very low concentrations. The value of the half saturation constant (KS2) is small as a result.
In some instances, a non-growth substrate competes with the growth substrate for enzyme active sites. Competitive Monod kinetics represent this situation. The equation representing primary substrate consumption is:
| (2.14) |
Where: k = maximum substrate utilization rate (M primary/M cells·T) X = biomass concentration on a pore volume basis (M/L3) C1 = concentration of primary substrate (M/L3) C2 = concentration of secondary substrate (M/L3) Ci = concentration of inhibitor (M/L3) KS1 = saturation constant for primary substrate (M/L3) KS2 = saturation constant for secondary substrate (M/L3) KSi = saturation constant for inhibitor (M/L3)
The stoichiometry equation for a biological process represents the conversion of mass from one form to another. These equations group into three major biological processes: biomass growth, biomass decay, and cometabolic transformation.
The biomass growth process includes growth of biomass, substrate consumption, and product formation. A typical equation representing this process is:
| (2.15) |
Where: X = biomass concentration on a pore volume basis (M/L3) Y = yield coefficient (M cells/M primary substrate) C2 = concentration secondary substrate (M/L3) C1 = concentration primary substrate (M/L3) F = stoichiometric ratio of secondary substrate to primary substrate
for biomass synthesis (M secondary/M primary)
The rate of Equation (2.15) can be described by any of the rate equations presented above (Equations (2.10) through (2.14)). For example, the double Monod rate equation can represent methanotrophic growth in the subsurface. Methane is the primary growth substrate while oxygen is the secondary growth substrate.
Biomass decay includes decay of biomass and the consumption of substrates needed to complete the process. A typical equation representing this process is:
| (2.16) |
Where: , decay rate of biomass (M/L3·T)
X = biomass concentration on a pore volume basis (M/L3) C1 = concentration primary substrate (M/L3) dc = primary substrate demand for decay (M primary/M cells) fd = biodegradable fraction of biomass (M/M) b = biomass decay rate (M biomass decayed /M biomass)
The biomass decay rate is typically a first-order or single Monod relationship. The above equation can include consumption of a substrate in the decay process; this is typically an electron acceptor. For example, decay of methanotrophic bacteria uses a single monod rate equation where oxygen is the electron acceptor (primary substrate).
Cometabolic transformation is the process mediated by microbes in which a non-growth substrate is converted from one form to another. Sometimes this transformation includes side-effects such as intermediate toxicity. Intermediate toxicity is a process that damages or inactivates microbes during the degradation of certain toxic contaminants. A typical equation representing the stoichiometry of this process is:
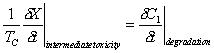 |
(2.17) |
Where: X = biomass concentration on a pore volume basis (M/L3) C1 = concentration degraded substrate (M/L3) TC = transformation capacity coefficient
(M cells destroyed /M substrate degraded)
Often this process is competitive with the growth process and uses the competitive Monod rate equation. For example, cometabolic transformation of TCE by methanotrophs uses Equation (2.14) for the rate equation where the primary substrate is TCE, the secondary substrate is oxygen, and the inhibitor is methane. In addition, TCE degradation creates a toxic intermediate product, TCE-Epoxide, which destroys biomass.
Biological processes also play an indirect role in the mass transport processes by changing material properties. Studies by Taylor and Jaffé (1990b), Taylor et al. (1990d) and Rittmann (1993) indicate that biomass growth affects material porosity, permeability, and dispersitivity values.
The following tables present biological parameter values found in literature for the processes described above.
Table 2.3.1 Sample Values for Single Monod Kinetic Substrate Consumption Parameters
| Source | Substrate |
k (d-1) |
KS1 (mg/l) |
Experiment |
|---|---|---|---|---|
| Alvarez-Cohen et al. (1993) | TCE | 0.31 | 1.1 | Laboratory |
| Strand et al. (1990) | Methane | 1.13 | 0.67 | Laboratory |
| Broholm et al. (1992) | Methane | 1.72 | 0.2 | Laboratory |
| Taylor and Jaffé (1990a) | Methanol | 7.70 | 0.799 | Column |
For a comprehensive review of Single Monod kinetic parameters, see Fry and Istok, 1994.
Table 2.3.2 Sample Values for Double Monod Kinetic Substrate Consumption Parameters
| Source | Primary |
k (d-1) |
Ks1 (mg/l) |
Secondary |
Ks2 (mg/l) |
Study |
|---|---|---|---|---|---|---|
| Srinivasan et al. (1988) | Creosote | 0.87 | 0.1 | Oxygen | 0.1 | Model |
| Semprini & McCarty (1991) | Methane | 1.2 - 2.0 | 1.0 - 2.0 | Oxygen | 1.0 | Model |
| Semprini & McCarty (1991) | Methane | 3.5 - 5.0 | 0.2 - 0.3 | Oxygen | .01 - 0.1 | Model |
| Lindstrom et al. (1992) | -- | 4.34 | 0.12 | Oxygen | 7.7 x 10-4 | Model |
| Dhawn et al. (1993) | -- | 4.8 | 1.0 | Oxygen | 1.0 | Model |
| Chen, Y-M, et al. (1992) | Benzene | 8.3 | 12.2 | Oxygen | 0.1 | Column |
| Chen, Y-M, et al. (1992) | Toluene | 9.9 | 17.4 | Nitrate | 2.6 | Column |
| Chen, Y-M, et al. (1992) | Toluene | 9.9 | 17.4 x 10-6 | Oxygen | 0.1 | Column |
Table 2.3.3 shows some biomass growth parameters used both in single and double Monod studies.
Table 2.3.3 Sample Values for Biomass Growth and Decay
| Source | Y (mg Cell/mg Sub) |
b (day-1) |
Study |
|---|---|---|---|
| Broholm et al. (1992) | 0.2 | 0.12 | Laboratory |
| Chen, Y-M, et al. (1992) | 0.5 | 0.1 | Column |
| Dhawn et al. (1993) | 1.0 - 0.5 | 0.024 | Model |
| Lindstrom et al. (1992) | 0.278 | 0.02 | Model |
| Semprini & McCarty (1991) | 0.35 - 1.1 | 0.15 - 0.40 | Literature |
| Semprini & McCarty (1991) | 0.5 | 0.10 - 0.15 | Model |
| Strand et al. (1989) | 0.51 | -- | Laboratory |
| Taylor and Jaffé (1990a) | 0.0975 | 0.0275 | Column |
The above tables represent only a small portion of the available literature on bioremediation parameters. These values were found in literature involving modeling efforts. Even within this narrow scope, the values of these parameters still span over a large range. For example, the biomass yield coefficient varies from 0.1 to 1.0 mg cells/mg substrate and the biomass decay rate from 0.02 to 0.15 d-1.
| [Home] | [Table of Contents] | [Prev. Page] | [Next Page] |
| A Two Dimensional Numerical Model for Simulating the
Movement and Biodegradation of Contaminants in a Saturated Aquifer © Copyright 1996, Jason E. Fabritz. All Rights Reserved. |
|||