The model uses the linear integrated (LI) method to calculate the change in concentration due to kinetic reactions. The LI method assumes that the rate of change in concentration over a time period remains constant, but allows it to change between time intervals. This linearization simplifies the calculation of changes in concentration, especially when reaction rates are dependent upon multiple species. Appendix D presents a detailed discussion of the LI method. The equation for change in nodal concentration due to kinetic reactions is:

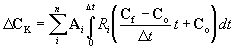(3.9)

Where:	DCK = change in concentration array due to kinetic reactions
	Cf = concentration array at beginning of timestep
	Co = concentration array at end of timestep
	Ai = stoichiometric array of the ith reaction
	Ri = rate function of the ith reaction
	D t = time step
	n = number of kinetic reactions

Equation (3.9) uses vector notation because some reaction rates can be a function of multiple species, and may change more than one species at a time.

Equation (3.9) also shows that DC_K is a function of both the initial and final concentrations and the length of the timestep. This is one of the reasons for the iterative nature of the solution of equation (3.5). The other is due to the nature of the equilibrium reactions.

The model uses the timestep calculated for the stability of the advection and dispersion calculation (Equation (3.8)). However, on certain occasions when reaction rates are rapid compared to the chosen timestep, the iterative method used to solve equation (3.9) will not converge. The model responds to this problem by cutting the timestep used in equation (3.9) in half and calculating the final concentration (C_f) for each sub-timestep.