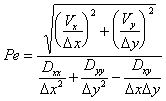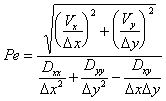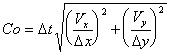[TOC]     4.3 Use of Dimensionless Variables [Prev. Page]   [Next Page]

The use of dimensionless variables for representing and calculating stability criteria is common in groundwater modeling. Dimensionless variables have the advantage of remaining independent of time and space scales. This chapter presents results as a function of three dimensionless variables; the Peclet number (Pe), the Courant number (Co), and the Damkohler number (Da).

The Peclet number relates the strength of advective forces relative to dispersive forces in the simulation. The Peclet number for a two-dimensional simulation is:

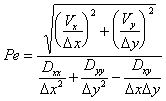(4.2)
Where: Vx,Vy = pore water velocity in X and Y directions (L/T)
  Dx = grid spacing in the X direction (L)
  Dy = grid spacing in the Y direction (L)
  Dxx = principal dispersion coefficient in the X direction (L2/T)
  Dyy = principal dispersion coefficient in the Y direction (L2/T)
  Dxy = cross dispersion coefficient (L2/T)

The Courant number relates to amount of advection relative to the grid mesh size. The Courant number for a two-dimensional simulation is:

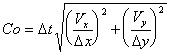(4.3)
Where: Dt = time step (T)
  Vx,Vy = pore water velocity in X and Y directions (L/T)
  Dx = grid spacing in the X direction (L)
  Dy = grid spacing in the Y direction (L)

The Damkohler number relates the rate of solute decay to advection. The Damkohler number in one dimension is:

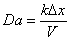(4.4)
Where: k = first order decay rate (T-1)
  D x = grid spacing (L)
  V = pore water velocity (L/T)
[Home]   [Table of Contents] [Prev. Page]   [Next Page]
A Two Dimensional Numerical Model for Simulating the Movement and Biodegradation of Contaminants in a Saturated Aquifer
© Copyright 1996, Jason E. Fabritz. All Rights Reserved.