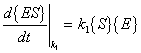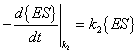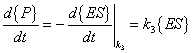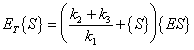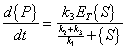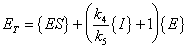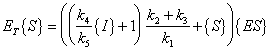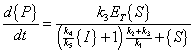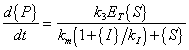Before describing the particular implementations of the various types of kinetics, it is necessary to review the theory behind Monod kinetics. Monod kinetics are different from, but still based upon Michaelis-Menten kinetics for enzymes. One can think of Monod Kinetics as describing a chain of enzymatically mediated reactions with a limiting step described by Michaelis-Menten kinetics. This is why the equations for both kinetic models are identical. The following paragraphs describe the development and theory behind Michaelis-Menten kinetics.

The basic assumption behind Michaelis-Menten Enzyme kinetics is that enzymes catalyze reactions by first forming an enzyme-substrate complex (Grady and Lim, 1975). This substrate complex will either decay back to enzyme and substrate (the reverse of the previously mentioned reaction) or irreversibly decay to enzyme and product. These chemical reactions for complex formation and product formation respectively are:

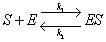	(A.1)
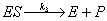	(A.2)

Where:	S = substrate
	E = enzyme
	ES = enzyme-substrate complex
	P = product
	k1 = rate constant for complex formation
	k2 = rate constant for reverse complex formation
	k3 = rate constant for product formation

The rates for the above reactions would be as follows:

	(A.3)
	(A.4)
	(A.5)

Where:	k1 = rate constant for complex formation
	k2 = rate constant for complex reverse formation
	k3 = rate constant for product formation
	{S} = concentration of substrate
	{E} = concentration of free enzyme
	{ES} = concentration of substrate-enzyme complex
	{P} = concentration of product concentration

Furthermore, it is assumed the above set of equations are in equilibrium such that:

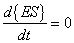(A.6)

Therefore:

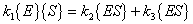(A.7)

A mass balance on the total enzyme is given as:

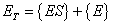(A.8)

Combining equations (A.7) and (A.8) and substituting into equation (A.5) gives:

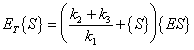(A.9)

and

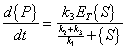(A.10)

so let

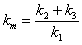(A.11)

therefore

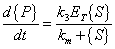(A.12)

Where:	{P} = concentration of product
	{ES} = concentration of enzyme-substrate complex
	{S} = concentration of substrate
	ET = total complexed and un-complexed enzyme
	k1 = rate constant for complex formation
	k2 = rate constant for reverse complex formation
	k3 = rate constant for product formation
	km = "half-saturation" concentration

Which is analogous to Monod kinetics, k₃ is analogous to the maximum specific substrate utilization rate, E_T is analogous to biomass concentration, and k_m is analogous to the half saturation constant. Monod kinetics and its variations, along with other bio-kinetic equations will be presented in the following discussion.

In competitive inhibition an inhibitory complex can combine with the controlling enzyme in addition to the reaction equation (A.1). This additional complex prohibits the enzyme from forming the complex with the substrate of interest.

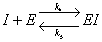(A.13)

Where:	I = inhibitor
	E = enzyme
	EI = enzyme-substrate complex
	P = product
	k4 = rate constant for complex formation
	k5 = rate constant for reverse complex formation

Equation (A.8) now looks like:

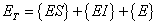(A.14)

Where:	ET = total complexed and un-complexed enzyme
	{E} = concentration of free enzyme
	{ES} = concentration of substrate-enzyme complex
	{EI} = concentration of inhibitor-enzyme complex

After substitution of equation (A.13) (with the assumption of equilibrium) equation (A.14) becomes:

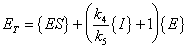(A.15)

The same derivation for Michaelis-Menten Kinetics as presented above applies:

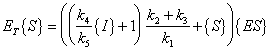	(A.16)
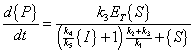	(A.17)

so let

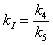(A.18)

therefore

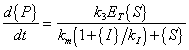(A.19)

Where:	{P} = concentration of product
	{ES} = concentration of enzyme-substrate complex
	{S} = concentration of substrate
	{I} = concentration of inhibitor
	ET = total complexed and un-complexed enzyme
	k1 = rate constant for complex formation
	k2 = rate constant for reverse complex formation
	k3 = rate constant for product formation
	km = "half-saturation" concentration
	kI = "saturation" constant for inhibitor

There are other types of inhibition, such as un-competitive, and substrate inhibition which are not presented here.

Semprini (1991) studied the competitive inhibition of TCE degradation by methane. A double Monod form of inhibition kinetics was used:

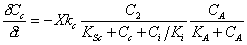(A.20)

Where:	Cc = concentration of contaminant
	Ci = concentration of the inhibitor
	CA = concentration of the electron acceptor
	KSc = saturation constant for contaminant
	KA = saturation constant for the electron acceptor
	kc = maximum transformation rate
	Ki = inhibition constant

It should be noted equation (A.20) is in the form of double Monod kinetics, however, the first term in the equation is the same form as equation (A.19). The second order electron acceptor term was included since the presence of an electron acceptor was required for the contaminant transformation.