| [TOC] | Appendix B Integrated Operator-Splitting Method | [Prev. Page] | [Next Page] |
In 1992, Valocchi and Malmstead (V&M below) explored a mass balance error inherent in the standard operator-splitting method. In their analysis, they proposed an "alternating" operator-splitting method to reduce mass balance errors at a constant concentration boundary. This thesis proposes a second alternative, integrated operator-splitting.
This appendix will describe the integrated operator-splitting method (IOS) and conduct the error analysis of V&M. The results of the IOS error analysis will be compared to those of standard OS.
Before conducting the error analysis it is necessary to describe IOS and how it differs from OS. In OS the advection-dispersion processes are de-coupled from the reaction processes. The advection-dispersion problem is solved first, resulting in an intermediate concentration. This intermediate concentration is used as the initial concentration for the reaction problem. The reaction problem is solved over the same timestep resulting in the final concentration at the end of the timestep. IOS eliminates the use of the intermediate solution. Instead, it uses the change in concentration calculated in the advection-dispersion step as a source/sink term in the system of reaction equations. It was speculated that using the initial concentration at a timestep and accounting advection and dispersion implicitly in the reaction equations would reduce the error in the final solution. It will be shown later, for the case of a one-dimensional aquifer with a continuous source of a non-conservative solute, the error in IOS is lower than OS.
The discrete form of equation (3.1) is used to calculate the change in concentration at a node over a given timestep is:
| (B.1) |
Where: DC = change in concentration over a time interval Cf = concentration at end of time interval Ci = concentration at beginning of time interval DCF = change in concentration due to advective-dispersive flux DCrxn = change in reaction due to kinetic reactions
It should be noted the solution to the kinetic reaction equation uses the linear integrated method described in Appendix D. Table B.1 describes the steps used to solve equation (B.1).
Table B.1 IOS Order of Calculation
| Step | Compute | Comment |
|---|---|---|
| 1 | D CF = f(Ci,D t) | Compute the change in concentration at a node due to conservative advective-dispersive flux |
| 2 | Cf = Cio + D CF | Compute a trial final concentration, it is needed for the calculation of kinetic reactions. |
| 3 | D Crxn = f(Ci,Cf,D t) | Compute the change in concentration due to kinetic reactions, which is a function of initial and final concentrations, and the length of time period. |
| 4 | D C = D CF + D Crxn | Compute the trial change in concentration at the node |
| 5 | Cf = Ci +D C | Compute new trial final concentration. If the change in Cf from the last iteration is not sufficiently small, go back to step 3 and continue iteration. |
Having described the IOS method, the error analysis used by V&M can be conducted. First consider a one-dimensional aquifer with a constant source of solute undergoing first order decay. The boundary and initial conditions are:
| (B.2) | |
| (B.3) |
and the equation of first order decay is:
| (B.4) |
To determine the change in concentration due to first order decay over the timestep, D t, using the LI method, the following integration is performed:
| (B.5) | |
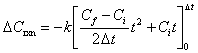 |
(B.6) |
| (B.7) |
Since first order decay is a relatively simple reaction, the final concentration, Cf , can be determined directly, it will not be necessary to perform the iterative procedure outlined in Table B.1. Since Cf = Ci + D CF + D Crxn equation (B.7) becomes:
| (B.8) | |
| (B.9) | |
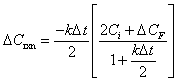 |
(B.10) |
| (B.11) |
At the end of the first timestep the simulation equation (B.1).becomes:
| (B.12) |
Solving for the final concentration:
| (B.13) |
Now substituting C*(X,D t) for Ci + D CF to change (B.13) into a form similar to equation (12) in V&M yields:
| (B.14) |
Since in the first time step, Ci = 0, equation (B.14) becomes:
| (B.15) |
C*(x,D t) is the "perfect" solution to the advective-dispersive equation at the end of timestep D t at location x. Now continuing with the IOS form of equation (15) of V&M:
| (B.16) | |
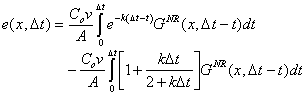 |
(B.17) |
Simplifying:
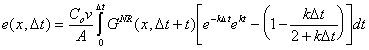 |
(B.18) |
Integrating the above equation over an infinite aquifer;
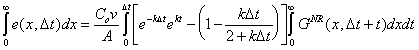 |
(B.19) |
leads to the mass balance error over the entire aquifer at the first timestep, D t:
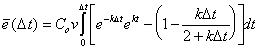 |
(B.20) |
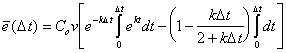 |
(B.21) |
| (B.22) |
To find the relative mass error, it is necessary to divide by total mass in the system:
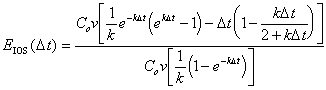 |
(B.23) |
Which reduces to the relative cumulative mass balance error at the first timestep, D t.
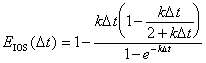 |
(B.24) |
Which is a function of kD t, the same as the error term derived by V&M for standard OS. Figure B.1 illustrates the differences in error between these two methods. It should be noted, the IOS error is reported as an absolute value. The IOS error is negative in value but less in magnitude than OS.
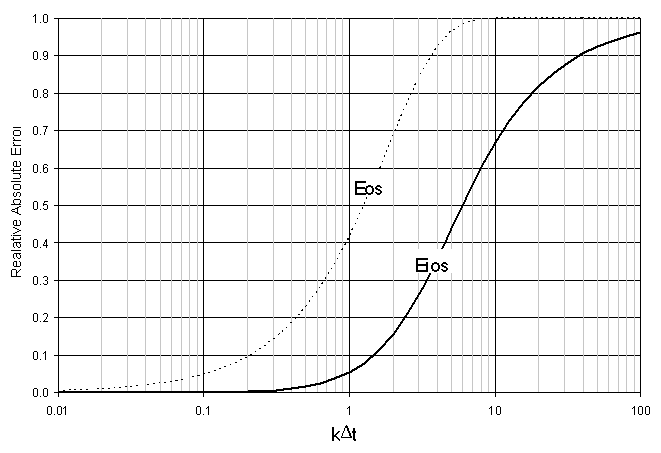
Figure B.1 Comparison of IOS and OS Error as a Function of kD t..
| [Home] | [Table of Contents] | [Prev. Page] | [Next Page] |
| A Two Dimensional Numerical Model for Simulating the
Movement and Biodegradation of Contaminants in a Saturated Aquifer © Copyright 1996, Jason E. Fabritz. All Rights Reserved. |
|||