This section evaluates model performance in simulating one-dimensional transport of a conservative solute resulting from an instantaneous source. It reports RSSE as a function of Peclet (Pe) and Courant (Co) numbers. The analytical equation representing solute transport in the aquifer is (Fetter, 1994):

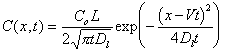(4.6)

Where:	t = time (T)
	x = distance from inlet (L)
	Co = initial concentration of pulse (M/L3)
	L = length of pulse application (L)
	V = pore water velocity (L/T)
	Dl = dispersion coefficient (L2/T)

Equation (4.6) makes the following assumptions about initial and boundary conditions:

• C(x,0) = 0.0 for x ¹ 0
• C(0,0) = Instantaneous Point Source of Infinite Concentration
• Infinite Aquifer Length
• Homogeneous Material Properties

Figure 4.5.1 illustrates log RSSE contours as a function of Peclet (Pe) and Courant (Co) numbers:

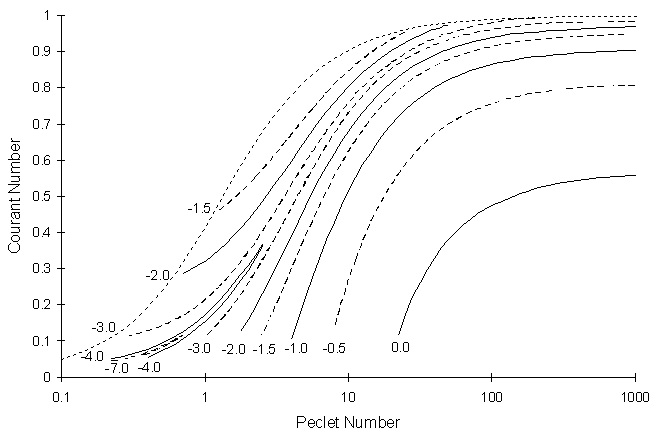
Figure 4.5.1 Log RSSE Contours as a Function of Pe and Co for One-Dimensional Conservative Solute Transport with a Pulse Source

Once again, Figure 4.5.1 shows that the RSSE is highly sensitive to the choice of Peclet and Courant number. It also shows that the region containing the lowest RSSE values corresponds to the region of no oscillations in Figure 3.8.3.

Figure 4.5.2 through Figure 4.5.4 illustrate concentration profiles for various combinations of Peclet and Courant numbers. The three figures illustrate choices of: low Courant and Peclet number; low Courant number and High Peclet number; and high Courant and Peclet number. Circles and lines represent numerical and analytical values respectively.

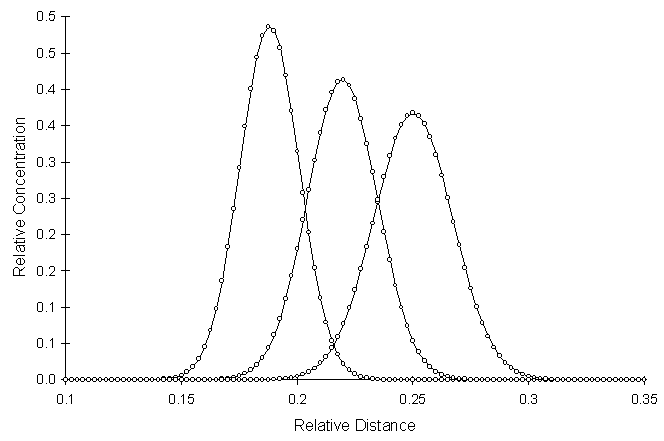
Figure 4.5.2 One-Dimensional Conservative Solute Transport with a Pulse Source, Pe = 2.5, Co = 0.36, RSSE = 2.6 x 10^-5

Figure 4.5.2 illustrates the choice of a low Courant and Peclet number. This combination of Courant and Peclet numbers falls in the region of no oscillations in Figure 3.8.3.

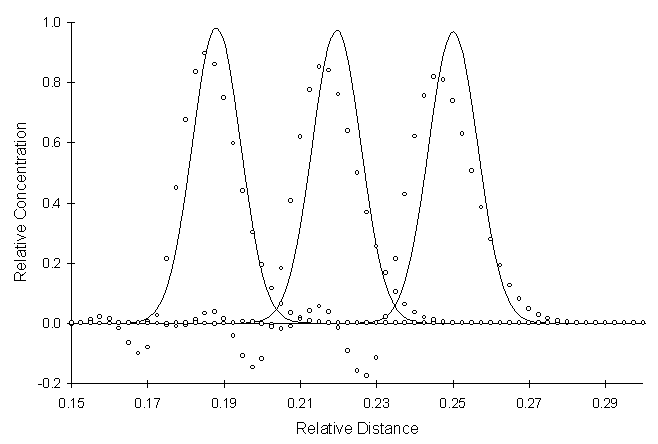
Figure 4.5.3 One-Dimensional Conservative Solute Transport with a Pulse Source, Pe = 250, Co = 0.36, RSSE = 1.4

Figure 4.5.3 illustrates a simulation with space oscillations. The choice of the Courant number is too low for the choice of Peclet number. This combination of Courant and Peclet number falls in the region of space oscillations in Figure 3.8.3.

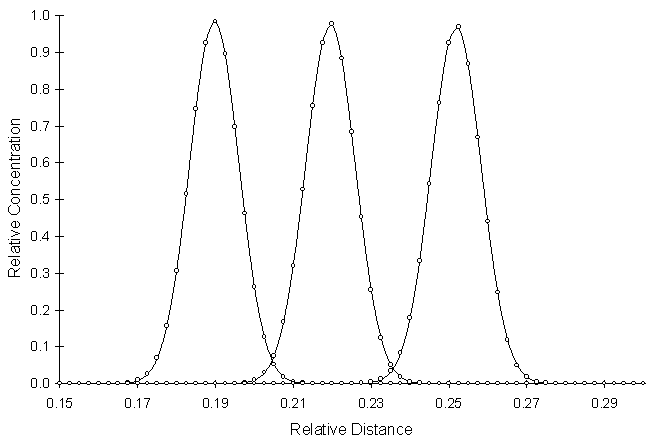
Figure 4.5.4 One-Dimensional Conservative Solute Transport with a Pulse Source, Pe = 250, Co = 0.995, RSSE = 7.3 x 10^-4

Figure 4.5.4 illustrates the simulation of highly advective system. The combination of Courant and Peclet number falls in the region of no oscillations.