There are many methods that could have been chosen to solve the reaction portion of the advection-dispersion-reaction equation in the operator-splitting scheme. Finite difference schemes could have been used. Odencrantz (1992) used a fourth order Runge-Kutta method using 5 to 100 sub-time steps for every advection-dispersion timestep. For this work, the linear integrated (LI) method was chosen. It is assumed this method is not new, however it is not known what it is otherwise called. The basic premise that underlies the LI method is that concentrations are assumed to only vary linearly over the given time step, D t. Equation (D.1) depicts the formula used to represent concentration as a function of time.

(D.1)

Where:	C = concentration as a function of time (t)
	Cf = final concentration
	Co = initial concentration
	D t = time step
	t = time

The final concentrations at the end of a time step are determined by substituting the linearized equation (D.1) into the reaction equations and then integrating over the time step. D t. An initial guess for the final concentration is used to determine the change in concentration due to each reaction in the system. Then, the individual integrated reaction rates are summed up to determine the net change in concentration due to reaction. The final concentration is then calculated as the initial concentration plus the net concentration change. The process is then repeated using this new final concentration. Iterations continue until the change in the final concentration between iterations is sufficiently small. This particular iterative method of the solution of the LI system of equations may not be the most efficient, but it is easy to code, and should return the same value as another method would.

In most chases the LI method will converge quickly. However, there are cases where reaction rates are large, they may cause concentrations to fall in the negative range. With certain reactions, this can cause an oscillatory effect in the calculations. A solution will not be found. To fix this problem, one only needs to decrease the size of the time step used in the calculation until a timestep small enough is found. This will break the effect.

For an example of the implementation of the LI method, consider a first order decay reaction:

(D.2)

Substituting equation (D.1) into equation (D.2) yields:

(D.3)

The LI method then requires integration over the time period, D t.

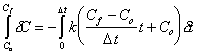(D.4)

which yields:

(D.5)

Due to the simplicity of the first order equation, the change in concentration is a function of the average of the initial and final concentration of the time step. Most equations however, are not this simple.

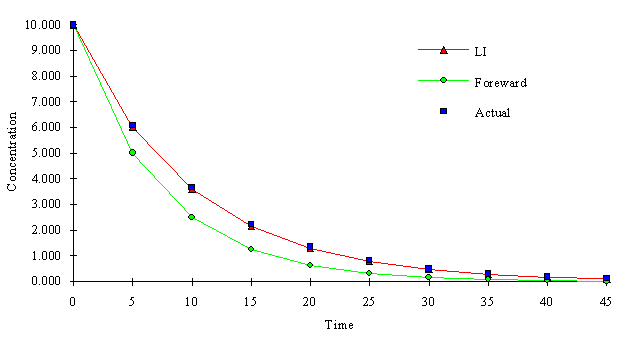
The following figure depicts the a comparison of a first order decay reaction using the LI method and a forward finite difference method. Both methods use k = -0.1 and D t = 5.0.

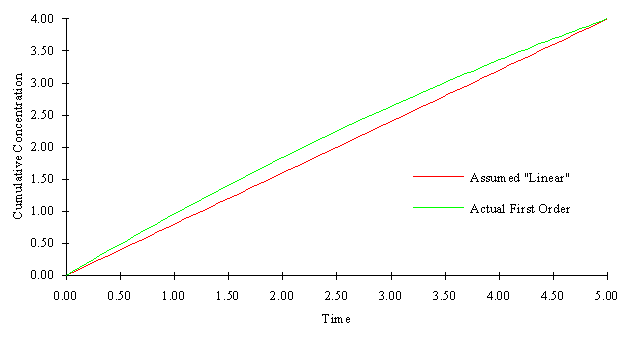
It may be necessary to analyze each reaction separately, and develop criteria for the maximum allowable time step in order to minimize errors. For example consider the first order reaction mentioned above. The following figure illustrates the difference in cumulative concentration change due to reaction between the assumed "linear" relationship and the actual first order relationship (assuming the only reaction occurring is the first order decay reaction). If the relationship varies too much from the linear line, it may be necessary to decrease the time step. The maximum allowable time step may be a function of how much deviation from linearity is allowed, and the magnitude of the reaction coefficients. However, analysis such as this were not included here, they were considered to be out of the scope of this work.